맨해튼 거리와 체비셰프 거리

오늘 백준 22878 간단한 문제를 풀었다. 흔히 택시 거리나 맨해튼 거리로 불리는 $L_1$ norm 문제다.

택시 거리를 만나면 습관적으로 45° 회전을 시킨다. 이 문제 역시 회전시켜 보니 케이스를 나눌 수 있다. 포함과 배제의 원리를 써서 문제를 $\min(a, b)=a+b-\max(a,b)$로 변형하면 평범한 2차원 스위핑 문제가 된다.

꽤 오래 고민해서 힘들게 풀었다. 그런데 solved.ac 난이도 투표에 들어갔더니 웰노운이란다. 나처럼 스크래치부터 푼 사람들은 대체로 다이아5 정도로 투표했다. 그런데 웰노운이란 사람들은 플래5까지 나왔다.

이게 도대체 뭔 소리인가? 알고 보니 내가 푼 방법과 똑같은 방법이다. 또 나만 모르는 웰노운이다.

까먹을까 봐 간단히 내용을 정리한다.

맨해튼 택시 거리는 $L_1$ norm이고, 체비셰프(chebyshev) 거리는 $L_{\infin}$ norm이다.

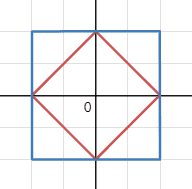
$L_p$ norm에 대해 안다면 $L_1$ norm과 $L_{\infin}$ norm이 비슷하게 생겼단 걸 알 것이다. 둘 다 contour를 보면 정사각형 모양이다. 회전하고 크기를 바꾸면 딱 알맞을 것 같다.

실제로 그렇다. 좌표를 45° 회전시키고 $L_1$ norm을 구하면 $L_{\infin}$의 두 배가 나온다. 즉 다음과 같다:

$\max(|x|,|y|)=\frac{1}{2}|x+y|+\frac{1}{2}|x-y|$

증명이 궁금하다면 $(|x+y|,|x-y|)$의 $L_1$ norm을 식 정리만 하면 되니 직접 해보자.

결국 위 문제는,

$\min(|p|,|q|)=|p|+|q|-\max(|p|,|q|)=|p|+|q|-\frac{1}{2}|p+q|-\frac{1}{2}|p-q|$

이므로 택시 거리를 두 번 구하는 게 맞다.

택시 거리에 관한 재밌는 법칙이니 기억해두자.